0%

(2017) MentorNet:Regularizing Very Deep Neural Networks on Corrupted Labels

Posted on Edited on In , ,

Keyword [SPADE]

Jiang L, Zhou Z, Leung T, et al. MentorNet: Regularizing Very Deep Neural Networks on Corrupted Labels[J]. arXiv preprint arXiv:1712.05055, 2017.


1. Overview

1.1. Motivation

  • DNN can remember entire data which are labeled randomly
  • DNN has more parameters than the number of training example
  • Poor performance when overfit noise
  • Curriculum Learning. gradually learn samples in a meaningful sequence

In this paper, it proposed MentorNet and SPADE (SG-partial-D) algorithm

  • first study to learn a curriculum (weighting schema) from data by neural network
  • supervise the training of StudentNet, improve the generalization on corrupted training data


  • learn time-varying weights for each example to train StudentNet, result in a curriculum that decide the timing and attention to learning each example



1.2. Step

  1. pretrain MentorNet to approximate predefined weighting specified in labeled data
  2. finetune MentorNet on the third clean label dataset
  3. train StudenNet using fixed MentorNet
  4. StudenNet make prediction without MentorNet

1.3.1. Model Regularizer

  • less effective on corrupted label.
  • weight decay
  • data augmentation
  • dropout

1.3.2. Data Regularizer

tackle in the data dimension.

  • MentorNet.
  • foucs on weighting example in corrupted labels.
  • can understand and further analyzed existing weighting schemes (self-paced weighting, hard negative mining, focal loss).

1.3.3. Weight Schemes

  • Curriculum Learning
  • Mine hard-negative example
  • Training a network using clean data, coupled with a knowledge graph, to distill soft logits to the noisy data

1.4. Model

Goal

  • overcome overfitting by introducing a regularizer to weight example
  • alternately minimize w and v (fix one, update another)


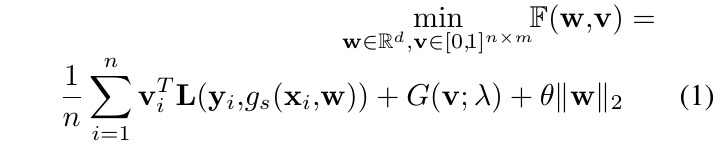
  1. Weighted Loss (WL)
    1. v (n samples x m classes). weight of examples
    2. L. loss
    3. g_{s}. StudentNet
  2. Explicit Data Regularizer (G). which contains two forms, both lead to same solution.
    1. explicit. analytic form of G(v)
    2. implicit. closed-form solution. v^{*} = argmin_{v} F(w, v) (F can be MentorNet)
  3. Weight Decay

1.5. Algorithm

  • Problems
    • fix v update w. wasteful when v is far away from optimal point
    • fix w update v. matrix v is too large for memory
  • SPADE
    minimize w and v stochastically overmini-batches.


  1. (5) moving average on the p-th percentile
  2. (8) weight decay
  3. (9) SGD or other optim


2. MentorNet

2.1. Goal

  • learn optimal Θ to compute the weight of example
  • step. pretrain - finetune - fix and plug in Algorithm

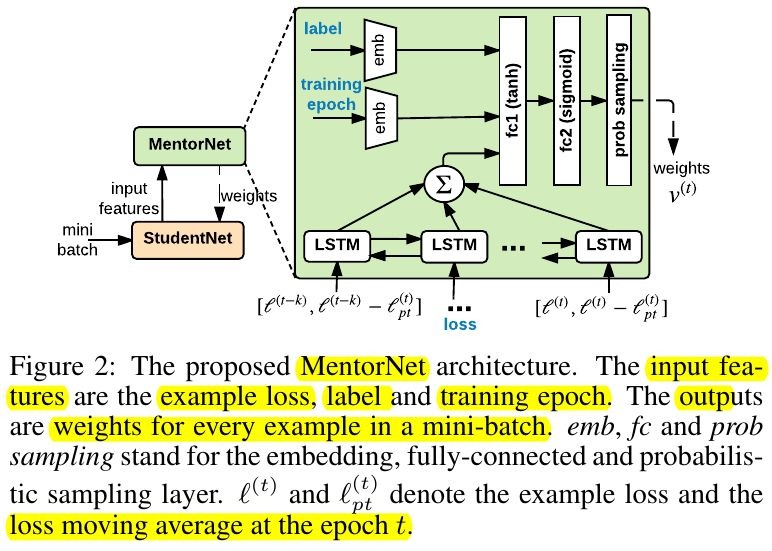
2.2. Architecture




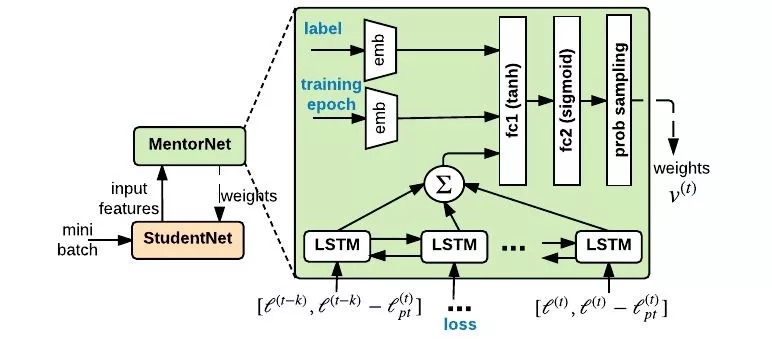
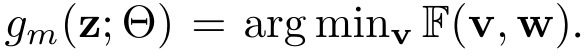
2.2.1. Input z

  • label
  • epoch
  • absolute loss
  • moving average

2.2.2. Sampling Layer

  • sample the weights v, without replacement, according to the normalized weight distribution
  • only perform on trained MentorNet
  • sampling rate. hyperparameter

2.3. Pretraining

2.3.1. Dataset

  • enumerate the input space of z, and annotate a weight for each data point
  • weight can derived from any weight schemes

2.3.2. Objective Function

  • (5). explicit
  • (6). converge fast
  • converge to the same solution


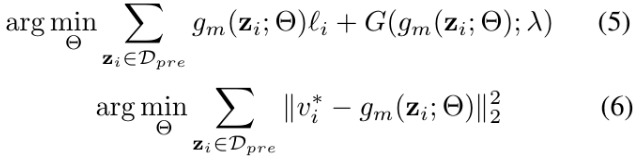
2.4. Finetuning

The weighting schemes may change along with the learning process of StudenNet.

  • Dataset
    • sample from dataset D
    • binary label for whether learn this example


3. Experiments

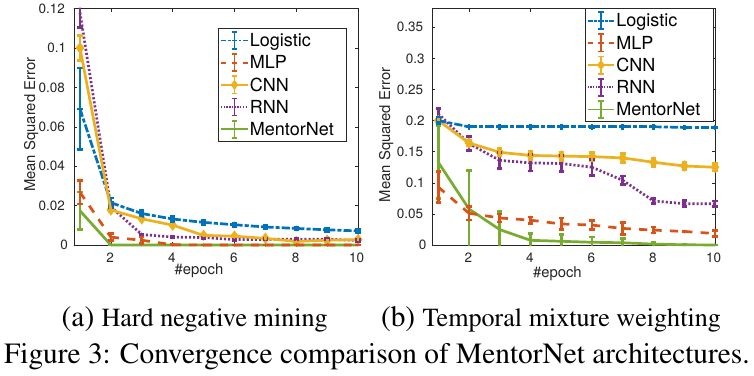
3.1. Other network

  • label weight according to different weighting schemes



3.2. Other regularizer




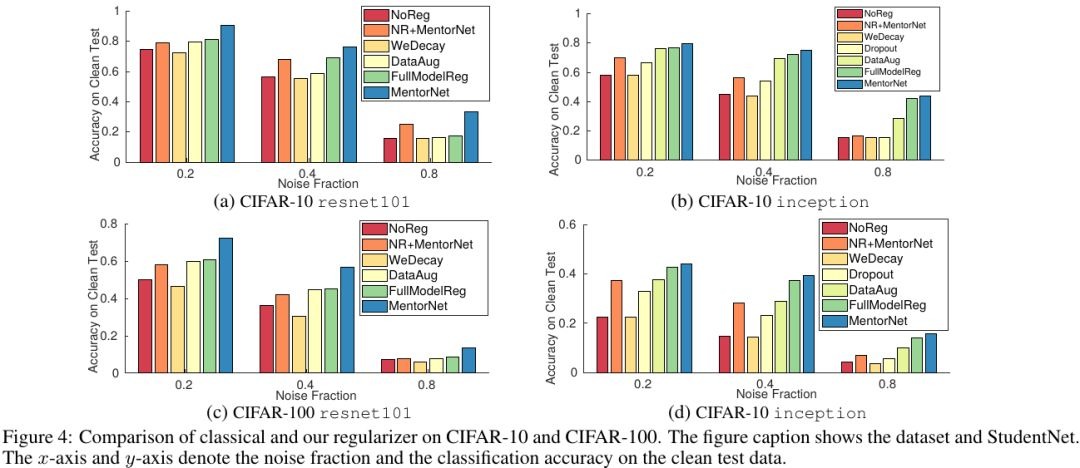
  • (b). Weighted loss converge to zero


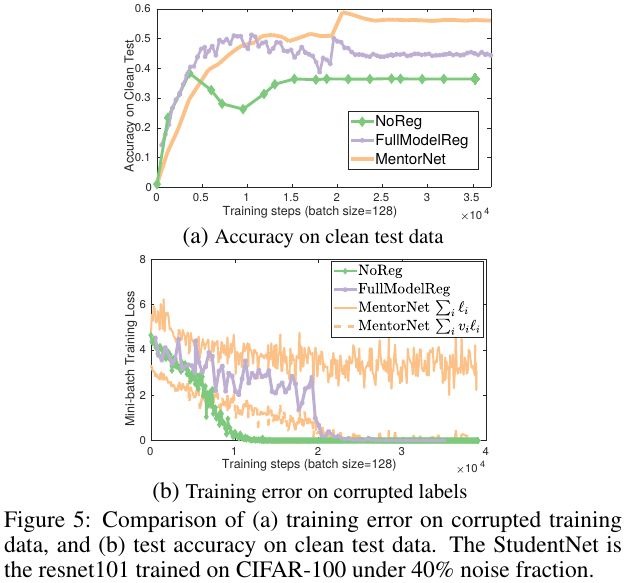
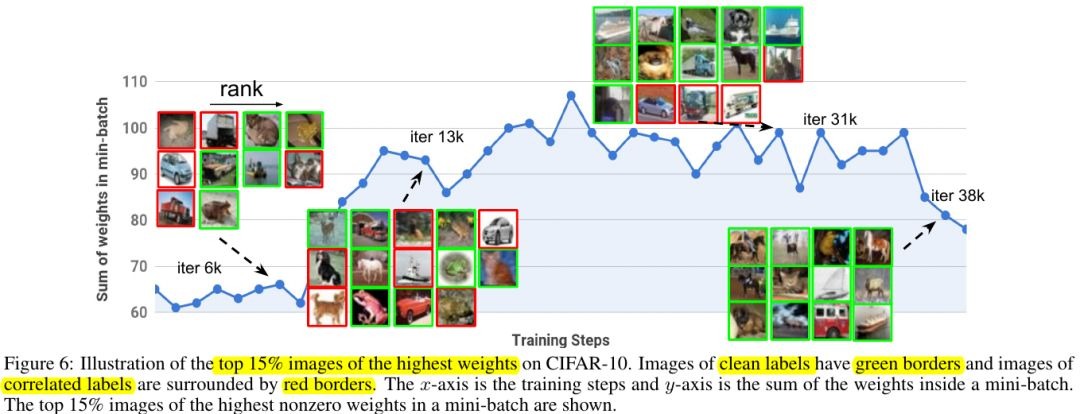
3.3. Representation of MentorNet

  • similar images have less distance.